| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- Zotero
- LaTeX
- 수식삽입
- 논문작성법
- Linear algebra
- matplotlib
- Julia
- pytorch
- JAX
- MATLAB
- obsidian
- teps
- 옵시디언
- Dear abby
- 논문작성
- 딥러닝
- 수치해석
- 인공지능
- 에러기록
- Python
- 우분투
- ChatGPT
- Statics
- WOX
- 생산성
- Numerical Analysis
- IEEE
- 텝스
- 고체역학
- 텝스공부
- Today
- Total
목록수학 Mathematics (34)
뛰는 놈 위에 나는 공대생
 [응용선형대수] Linear independence, basis and dimensions
[응용선형대수] Linear independence, basis and dimensions
1. Introduction (위 그림 상에서 [0 1]은 $\begin{bmatrix}0&1\end{bmatrix}^{T}$와 같다는 것에 유의해주세요) 한 vector $\begin{bmatrix}x&y\end{bmatrix}^{T}$가 있을 때 $x\begin{bmatrix}1&0\end{bmatrix}^{T}+y\begin{bmatrix}0&1\end{bmatrix}^{T}$ 두 벡터(위 그림의 e1, e2)의 조합으로 모든 x,y에 대해 표현할 수 있습니다. 이 때 조합할 때 사용되는 계수 (x,y)로 unique하게 한 개밖에 없습니다. 예를 들어 $\begin{bmatrix}-2\\0\end{bmatrix}$를 표현하고 싶다면 $(-2)\times e1+0\times e2$ 외에 e1, e2..
 [확률및통계] 몬티 홀 문제와 문제 확장(문이 N개일 때)
[확률및통계] 몬티 홀 문제와 문제 확장(문이 N개일 때)
조건부확률과 베이즈 정리에 대해 설명할 때 대표적으로 등장하는 예시입니다. 몬티 홀 문제는 몬티 홀이라는 호스트가 진행하는 tv쇼가 배경입니다. 문이 총 3개가 있을 때 3개의 문 중 하나의 뒤에는 고급 차가 있고 나머지 문 뒤에는 염소가 있습니다. 사회자는 자동차가 어떤 문 뒤에 있는지 알고 있고, 참가자에게 문 하나를 선택하게 합니다. 참가자가 문을 하나 선택한 뒤, 사회자는 참가자가 선택하지 않은 문 중 하나를 열어서 염소가 있음을 보여줍니다. 그리고 문을 바꿀 기회를 줍니다. 참가자는 문을 바꾸는 것이 더 유리할까요? 아니면 문을 그대로 유지하는 것이 유리할까요? 단순하게 생각하면 바꾸든, 바꾸지 않든 확률의 차이가 없을 것 같지만 베이즈 정리를 통해 계산해보면 차이가 존재합니다. Backgrou..
1. Ax=b와 Column space&Null space 관계 이 column space와 null space 개념을 통해 $Ax=b$에 대해 이해해볼 수 있습니다. $\text{Given }Ax=b$ $\text{(i). C(A) provides information whether it has a solution. Ax=b has a solution }\Leftrightarrow$ $\begin{bmatrix}b_{1}\\b_{2}\\b_{3}\end{bmatrix}\in C(A)$ 만약 b matrix가 column space of A($C(A)$)에 속해있다면 A의 column들의 선형 조합으로 b를 만들 수 있다는 뜻이므로, x가 존재합니다. (x는 A의 column의 선형 조합에서 계수에 해당..
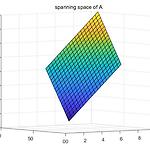 [응용선형대수] Null space/Column space
[응용선형대수] Null space/Column space
1. Definition of Null space $\text{Definition : }$ $\text{null space of A, }N(A)=\{x\in\mathbb{R}^{n},Ax=0\}$ $\text{claim }N(A)\text{ is a subspace}$ $\text{(i). non-empty }\Rightarrow$ 항상 $A\dot 0=0$이므로 null space에는 영벡터가 존재하고, null space은 empty일 수 없다. $\text{(ii). }Ax_{1}=0, Ax_{2}=0 \Rightarrow A(x_{1}+x_{2})=Ax_{1}+Ax_{2}=0$ $\text{if }x_{1},x_{2}\in N(A)\text{, then }x_{1}+x_{2}\in N(A)$ $\..
 [선형대수] Rectangular matrix의 곱과 singularity
[선형대수] Rectangular matrix의 곱과 singularity
보통 다루는 matrix가 square matrix라서 거의 생각을 안했는데 최근 제어 공부를 하다가 controllability matrix나 observability matrix가 rectangular matrix이어서 rectangular matrix에 대해서 좀 고민하게 되었습니다. 1. Rectangular matrix의 곱에서 singularity를 판별하는 문제 $A\in \mathbb{R}^{m\times n},B\in \mathbb{R}^{n\times m}\text{, where }m
앞에서 썼던 LU Decomposition 외에도 Cholesky decomposition, QR Decomposition, SVD(Singular Value Decomposition) 등 다양한 행렬분해가 존재한다는 사실을 알게 되었습니다. 가끔 시간 날 때마다 정리를 해두면 도움이 될 것 같아서 적어둡니다. 위키피디아(ko.wikipedia.org/wiki/%ED%96%89%EB%A0%AC_%EB%B6%84%ED%95%B4)에 따르면, 선형 방정식과 관련된 분해와 교윳값(eigenvalue)에 근거한 분해 2가지 종류의 분해가 대표적으로 쓰입니다. LU, QR, Cholesky decomposition은 선형 방정식과 관련된 분해이고, eigenvalue, jordan, singular value d..
참고하면 좋은 글 : normal-engineer.tistory.com/29 [고등자동제어] 제어에서 필요한 수학 개념 제어에서 많이 쓰이는 수학에 대해서 간단하게 정리합니다. 사실 상 전부 linear algebra 내용입니다. 1. Field F Definition : a set of elements called scalars together with two binary operations, additio.. normal-engineer.tistory.com 1. Vector space $\text{Vector space : abstract concept of }\mathbb{R}^{n}$ $\text{Let }V=\mathbb{R}^{n}$ $a=(a_{1},a_{2},\cdots,a_{n})$ $..
 [응용선형대수] LU Decomposition
[응용선형대수] LU Decomposition
앞에서 작성한 글을 참고하는 것을 추천드립니다. 이번에는 LU Decomposition에 대해서 다루겠습니다. LU Decomposition은 linear equation의 solution을 구할 때 도움이 되기 때문에 소개해드립니다. 이 글에서 말하는 LU가 무엇을 의미하느냐, $L\text{ : Lower triangular matrix}$ $U \text{ : Upper triangular matrix}$ 입니다. LU Decomposition 어떤 matrix A가 A = LU로 표현할 수 있다고 해보겠습니다. 우리가 앞서서 operation matrix 3가지를 살펴보았는데요, (자세한 내용은 아래 링크) normal-engineer.tistory.com/66?category=964340 [응용..
 [응용선형대수] 역행렬 구하기
[응용선형대수] 역행렬 구하기
역행렬을 구할 수 있는 방법에 대해서 정리합니다. 물론 2x2 matrix나 3x3 matrix까지는 이미 공식으로도 나와 있어서 굳이 여기서 설명하는 방법을 사용하지는 않아도 되지만 기억해두면 좋을 것 같습니다. 1. Three row operations 그 전에 gaussian elimination에 대해서 공부를 했었습니다. 자세한 내용은 아래 링크를 참고해주세요. normal-engineer.tistory.com/60?category=964340 [응용선형대수] Gauss elimination 가우스 소거법 앞의 글에서 linear equation에 대해서 보았고 해에 대한 3가지 경우를 살펴보았습니다. 복잡한 고차방정식에서도 해가 없는지, 무수히 많은지, unique solution이 존재하는지..
이번에는 Inverse matrix(역행렬)과 invertible의 성질에 대해서 정리합니다. 1. Inverse matrix 정의 $\text{Let A be an m x n matrix, if }\exists B\text{ such that }BA=I_{n}\text{, B is called a left inverse of A}$ $I_{n}\text{ is a n x n identity matrix}$ $\text{Let A be an m x n matrix, if }\exists C\text{ such that }AC=I_{m}\text{, C is called a right inverse of A}$ 만약 A가 square matrix가 아닌 rectangular matrix라면 left inv..
