수학 Mathematics/선형대수학 Linear Algebra

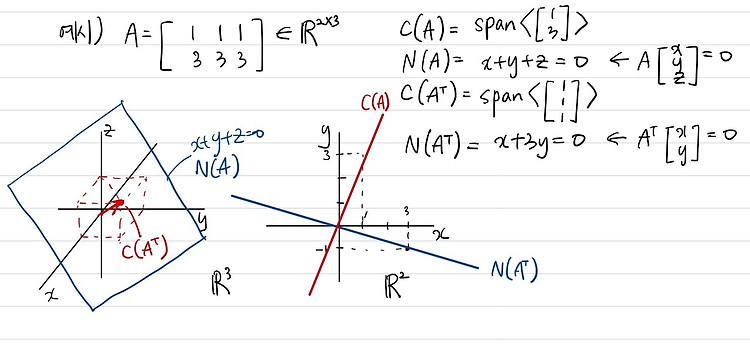
앞선 장에서는 projection과 cosine의 수학적 의미 등에 대해서 다루었다. 이번 장에서는 이러한 projection을 이용해서 space의 bases를 orthonormal bases로 바꾸는 방법에 대해 다룬다. 이렇게 하는 이유는 orthonormal bases일 때 가지고 있는 유용한 성질들 때문이다. Orthonormal bases $$\text{Def)}\quad q_1, \ldots, q_n \text{ are vectors and orthonormal if}\; q_{i}^{\top}q_{j}=\begin{cases}0 \; (i \neq j) \\ 1 \; (i=j)\end{cases}$$ $$ \text{Def)} Q \text{ is called an orthogonal ..

1. Inner products and cosines cosine의 물리적인 의미는 다음과 같이 이해할 수 있다. 위에서 벡터 b를 a에 대해 projection한 결과 (편의성을 위해 위의 벡터 표시는 생략) $p=\|b\| \cos\theta \dfrac{a}{\|a\|}=\dfrac{\|a\| \|b\|\cos\theta }{\|a\|^{2}}a=\dfrac{a^{\top}b}{a^{\top}a}a$ 첫번째 부등식은 그림을 보고 유도한 것이고 그 다음 등식은 내적과 cosine의 관계를 통해 유도된 것이다. 위를 통해 b를 a에 대해 projection한 결과는 $\dfrac{a^{\top}b}{a^{\top}a}$ 관계로 연결되어있음을 확인할 수 있다. 그러나 위의 결과는 2차원 평면에서 유도하는..

선형대수학에서 여러 matrix category가 있는데 맨날 정의를 잊어버리고 각 개념의 포함관계를 잘 알 수 없었다. 그래서 책(아래 참고문헌 적어놓음)을 참고하여 이번에 정리를 하고자 한다. 첫 번째 분류 1. Square / Non-square matrix matrix의 행과 열의 길이가 같으면 square matrix라고 한다. 그렇지 않은 non-square matrix는 선형대수학을 공부하면서 거의 다루지 않지만 dynamics를 공부하다보면 흔하게 나온다. 일반적인 경우에 변수와 방정식의 갯수가 일치하기가 쉽지 않기 때문이다. 그래서 이런 non-square matrix도 분석할 수 있는 Singular Value Decomposition(SVD)를 수행할 수 있다. SVD는 square ..

1. Length of vectors $\begin{bmatrix}x_{1}\\ \vdots\\ x_{n}\end{bmatrix}\in\mathbb{R}^{n}$ vector의 길이($\left \| x \right \|$)에 대한 식은 다음과 같습니다 $\left \| x \right \|=\sqrt{x_{1}^{2}+x_{2}^{2}+\cdots+x_{n}^{2}}=x^{T}x$ 2. Orthogonality $x,y\in \mathbb{R}^{n}$ x,y라는 n차원 벡터가 있을 때 두 벡터가 수직이라고 해보자. 피타고라스 공식에 의해 $\left \| x-y \right \|^{2}=\left \| x \right \|^{2}+\left \| y \right \|^{2}\cdots (1)$이 성립..

matrix의 처음 등장은 Linear equation을 matrix의 곱으로서 표현한다는 것에서 시작되었습니다. 그러나 matrix를 다른 관점에서도 이해할 수가 있습니다. 바로 matrix를 Linear transformations으로 해석하는 것입니다. $A : m\times n$ $A: \mathbb{R}^{n}\rightarrow \mathbb{R}^{m}$ $\text{ex) }$ 1) 벡터를 스칼라 c배 하는 것 $A=\begin{bmatrix} c&0\\0&c \end{bmatrix}$ $A\begin{bmatrix} x\\y\end{bmatrix}=\begin{bmatrix}cx\\ cy\end{bmatrix}$ 2) 벡터를 $y=x$ 대칭 $A=\begin{bmatrix}0 & 1\\..

응용선형대수에서 굉장히 중요한 개념인 Four fundamental subspaces Ax=b에서 b가 A의 matrix의 column space 안에 속해야 solution이 존재한다고 이야기했었고, null space 속한 vector를 더해도 Ax의 값에 영향을 미치지 못하므로 solution에 null space vector를 더한 것 역시 solution이 될 수 있었습니다. $A\bar{x}=b$인 $\bar{x}$는 solution입니다. 이 때 null space에 속한 벡터 $\tilde{x}(\Rightarrow A\tilde{x}=0)$가 있을 때 $\bar{x}+\tilde{x}$도 solution이 됩니다. $A(\bar{x}+\tilde{x})=A\bar{x}+A\tilde{x}..

1. Introduction (위 그림 상에서 [0 1]은 $\begin{bmatrix}0&1\end{bmatrix}^{T}$와 같다는 것에 유의해주세요) 한 vector $\begin{bmatrix}x&y\end{bmatrix}^{T}$가 있을 때 $x\begin{bmatrix}1&0\end{bmatrix}^{T}+y\begin{bmatrix}0&1\end{bmatrix}^{T}$ 두 벡터(위 그림의 e1, e2)의 조합으로 모든 x,y에 대해 표현할 수 있습니다. 이 때 조합할 때 사용되는 계수 (x,y)로 unique하게 한 개밖에 없습니다. 예를 들어 $\begin{bmatrix}-2\\0\end{bmatrix}$를 표현하고 싶다면 $(-2)\times e1+0\times e2$ 외에 e1, e2..

1. Ax=b와 Column space&Null space 관계 이 column space와 null space 개념을 통해 $Ax=b$에 대해 이해해볼 수 있습니다. $\text{Given }Ax=b$ $\text{(i). C(A) provides information whether it has a solution. Ax=b has a solution }\Leftrightarrow$ $\begin{bmatrix}b_{1}\\b_{2}\\b_{3}\end{bmatrix}\in C(A)$ 만약 b matrix가 column space of A($C(A)$)에 속해있다면 A의 column들의 선형 조합으로 b를 만들 수 있다는 뜻이므로, x가 존재합니다. (x는 A의 column의 선형 조합에서 계수에 해당..

1. Definition of Null space $\text{Definition : }$ $\text{null space of A, }N(A)=\{x\in\mathbb{R}^{n},Ax=0\}$ $\text{claim }N(A)\text{ is a subspace}$ $\text{(i). non-empty }\Rightarrow$ 항상 $A\dot 0=0$이므로 null space에는 영벡터가 존재하고, null space은 empty일 수 없다. $\text{(ii). }Ax_{1}=0, Ax_{2}=0 \Rightarrow A(x_{1}+x_{2})=Ax_{1}+Ax_{2}=0$ $\text{if }x_{1},x_{2}\in N(A)\text{, then }x_{1}+x_{2}\in N(A)$ $\..

보통 다루는 matrix가 square matrix라서 거의 생각을 안했는데 최근 제어 공부를 하다가 controllability matrix나 observability matrix가 rectangular matrix이어서 rectangular matrix에 대해서 좀 고민하게 되었습니다. 1. Rectangular matrix의 곱에서 singularity를 판별하는 문제 $A\in \mathbb{R}^{m\times n},B\in \mathbb{R}^{n\times m}\text{, where }m